法国有一个小女孩,放学回家后爸爸问她,“今天在学校学了什么啊?”
“今天学了 20×4+10+8。”小女孩回答道。
“那 20×4+10+8 等于多少呢?”爸爸继续问。
小女孩轻轻一笑,“20×4+10+8 等于 20×4+10+8。”

根据维基百科(WikiPedia)对 symbol(符号)这个词的解释,symbol 是希腊文里代表 token(象征)或 token of identity(身份的象征)之义的词,它结合了两个词根:sum(一起)和动词 ballo(丢掷)。对“符号”一词较宽松的诠释是“放在一起”。它的词源来自一种古老的证明方式,证明某人身份或某人与他人之间的关系。一根木棒或骨头被劈成两半,有关联的两人各取其半。为了核证这个关系,这两半必须完美地契合。
早在几万年前,智人就开始通过壁画来记录和传递信息。作为一种对现实世界的抽象表述,这些图形逐渐演变成了人类的语言和文字。大约三千年前,世界各地纷纷出现了用于记录的符号系统,不仅极大程度的增加了交流的简易性,也成为了记录知识的重要工具。而数学符号则和文字不同,一方面,数学符号虽然可以让书写更简洁和准确,但也增加了人们使用数学工具的门槛——必须要学习相应符号系统的含义才能入门;另一方面,数学符号所表示的并不是是现实世界中的存在,而是一种对抽象事物的抽象表示,也正因为如此,数学符号帮助我们实现了超越自然语言的思考方式。
用文字描述的数学
无论东方还是西方,数学的记录都比文学要早一千多年。世界上现存最古老的文字记录之一(德国考古研究院博物馆,编号W19408,76+)看起来像是在计算土地的面积。远在符号数字发明之前,人们就可以通过语言来描述数学计算的方法。欧几里得的《几何原本》就是完全用语言描述和几何图形完成的,这一巨著中甚至完成了 $(a+b)^2=a^2+b^2+2ab$ 这样复杂的证明:如果一个正方形的边长等于另外两个正方形的边长之和,那么这个正方形的面积就等于另外两个正方形面积之和加上由他们边长构成的长方形面积的两倍。
人们也可以用语言讲述和回答纯数字的问题,比如著名的丢番图的墓志铭:“这座石墓里安葬着丢番图。他生命的1/6是幸福的童年,生命的1/12是青少年时期。又过了生命的1/7他才结婚。婚后5年有了一个孩子,孩子活到他父亲一半的年纪便死去了。孩子死后,丢番图在深深的悲哀中又活了4年,也结束了尘世生涯。过路人,你知道丢番图的年纪吗?”。用语言描述的数学问题就已经很复杂了,更不用说用语言描述问题的解答。即使只是表达简单的数字,就像本篇开头的引文中所述的,在法语中98表示为“quatre-vingt-dix-huit”(四个二十、十以及八),文字也对使用者造成了许多不便和困扰。
聪明的中国人
在包含0的阿拉伯数字(印度数字)出现之前,数学的书写是非常繁杂的。一方面由于缺少占位符,许多时候不得不使用空格来表示,另一方面,一些数字符号如罗马数字,其左右顺序非常重要,因而连续写下多个数字时会发生混淆。直到今天,支票上也必须写下文字形式的数字来记录金额。
而古老的东方民族发明了以十进制为基础的数字记法,巧妙的避免了占位符合书写顺序的问题。中国文字使用了个,十,百,千,万这样的量词来表示数位,因此,像10086这样的数字可以表示为一万八十六,因而避免了缺乏占位符和同时书写多个数字发生混淆的问题。

中国人还发明了算筹来进行计算,算筹除了使用横竖杠来表示1-9的数字之外,还使用直式和横式的写法来表示数位,其中个、百、万、百万…数位采用直式,十,千,十万…数位采用横式,因此可以区分不同的数位。《孙子算经》中记载到:
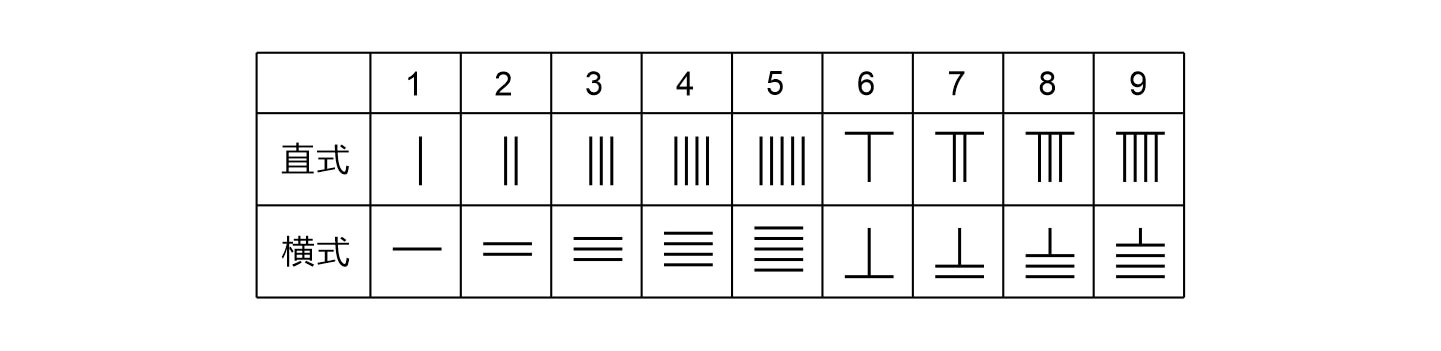
凡算之法,先识其位,一纵十横,百立千僵,千十相望,百万相当
来自印度的阿拉伯数字
令人难以置信的是,我们如今使用的阿拉伯数字直到16世纪才被广泛接受。说是阿拉伯数字,其实这一符号系统起源于9世纪的印度,一般认为,是费波那契的《计算书》将印度数字从阿拉伯传入欧洲。但早在《计算书》出现的一个世纪之前,花拉子米所著《还原与对消计算概要》的拉丁文译版就已经在西班牙出现,这也是已知最早的将印度——阿拉伯数字系统传入欧洲的书籍。
虽然阿拉伯数字在商业领域并不流行,但作为更先进的数字符号系统,它理应受到学术界的广泛关注。然而阿拉伯数字却迟迟没有流行,直到1543年,也就是哥白尼逝世那年,在他那年出版的著名著作《天体运行论》(De Revolutionibus Orbium Coelestium)当中,仍然有罗马数字、印度数字混用,甚至完全以文字书写数字的奇异现象。
伟大的韦达
《还原与对消计算概要》实际上是一本讨论如何求解一元二次方程(正)根的书,事实上,早在欧几里得的《几何原本》中,就写道通过配方的方式得到一元二次方程的根。花拉子米将一元二次方程分为几类,并给出了这些问题的解答方法,这些方法涉及到在方程(等式)的两边同时加上(或者减去)一项的消除操作。例如,
问题:将10分成两部分,其中一部分的平方是另一部分的81倍。
解答:10减去另一部分的平方等于10的平方加上这另一部分的平方减去这另一部分的20倍,将这20倍与81倍相加,可以得到100加此项的平方等于此项的101倍。将101减半得到50.5,将50.5的平方减去100得到2450.25;把它开方可以得到49.5,以101的一半减去49.5就可以得到这一项的大小为1。
这种解法涉及到了对负号的处理,而且花拉子米已经意识到,类似这样的方程都有两个根(其中一个可能是负数)。但由于对负数和零的认知恐惧,形如“平方与某物乘以一个未知数等于一个数”与“平方等于某物乘以一个未知数与一个数”一直以来都被认为是不同的方程。直到韦达引入了令人赞叹的“元音——辅音”记法,即用元音表示已知数,辅音表示未知数的方法,人们才意识到一元二次方程拥有形如 $ax^2+bx+c=0$ 的一般形式。
对我们而言,这样的表示似乎是再自然不过的,但对当时的人们来说,抽象地使用字母来表现涉及对象的更一般的特性,以及那些字母也可以和数字一样,遵从代数推导和法则的伟大想法,使得人们得到了思考与操作集体的、一般的、任意的(the any)、全部的(the all)的问题的方法,也“将代数提升到比便利的速记更高的层次”。
重新回归几何
算数(代数)最早是以几何形式出现在大家的视野当中的,随着发展逐渐与几何分开成为了单独的学科。直到韦达去世的三十四年之后,笛卡儿的《几何学》问世,代数和几何才重新被统一的认识。
值得注意的是,笛卡尔并不是最早发明和使用坐标系统的——早期的地理学家就会使用坐标系统,14世纪,就有利用经纬系统构造的坐标雏形。我们知道,加、减、乘、除以及平方开方的运算都可以化简为几何操作,例如 $a\times b$ 相当于求边长为 $a$ 和 $b$ 的长方形面积。然而这实际上是如何实现的呢?
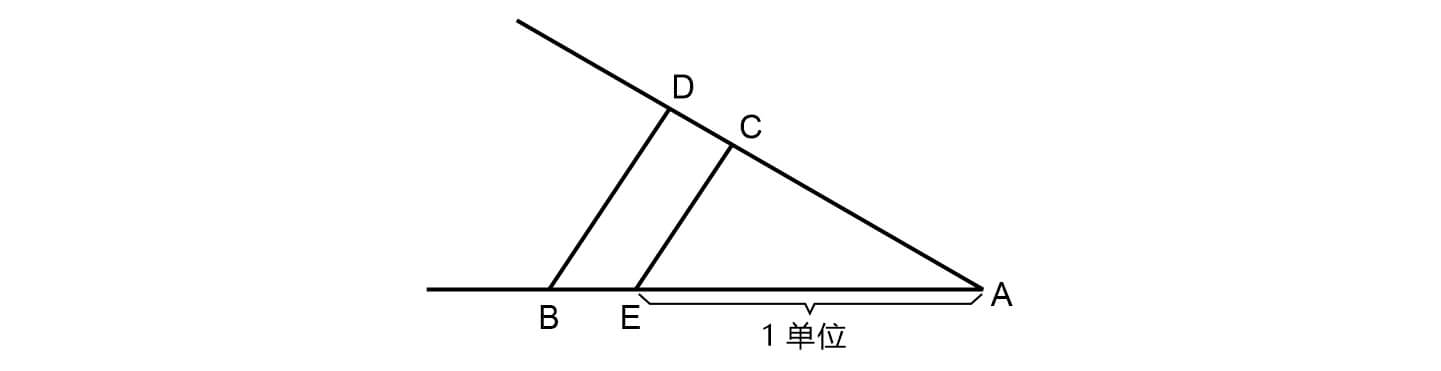
笛卡尔发明了一种把代数求解和尺规作图对应起来的方法,如图所示,在角A的两条边长分别作出边长为 $a$ 和 $b$ 的线段 AB 和 AC,在其中一条边上取单位长度 AE,连接 CE,过 B 点作 CE 的平行线与 AC 交于 D 点,AD 的长度就是乘积 $a\times b$。这不仅仅是几何到代数的一种对应,更实现了代数到几何的一种变换。
用同样的方法,三等分角的问题被等价为一个特殊的三次方程是否有有理数根的问题。笛卡儿无法得知这一答案,不过,我们知道:问题中的根并不存在。
莱布尼茨和牛顿
笛卡尔还改变了人们对曲线的理解,笛卡尔意识到,平面上的曲线是一系列点的运动的组合,这些点的位置(坐标)受到方程的约束,因而当其中一个坐标发生变化时,另一个坐标也会相应的发生变化。这种观点也成为了微积分的思想基础。
在17世纪初,也就是笛卡尔的《几何学》问世的时候,$+, -, \times, \div$ 这样的现代符号还没有被发明,$\sqrt{}, \ ^2$ 这样的标记方式尚未统一。甚至有哲学家认为,虽然符号的使用让书写变得简短,但反而增加了理解的负担,因为需要花很长的时间学习如何读懂符号背后的含义,相反古人在完成几何和算数上的证明时并不需要借助任何符号,因此符号是非必须的。
莱布尼茨则提出了不同的观点,他相信卓越的技法是理解人类思维本质的关键,“真正的方法”需要引导思维并帮助使用着完成计算。他耗时数年创造、调整和改善了许多符号,并尽可能的使用符号来让书写内容更清晰和明确。这其中就包括他为微积分所创立的符号 $\rm{d} x/\rm{d} y$ 以及 $\int$。莱布尼茨如此称赞自己的符号系统,
我认为,当这项工作完成后,它会是人类心智的最终成果,而众人皆将欢喜,因为他们将拥有一项得以颂扬智识的工具,如同望远镜让洞察更臻完美。
同一时期的牛顿也独立的发明了微积分方法,他使用 $\dot{x}$ 来表示微分。但牛顿对微积分的理解和莱布尼茨是完全不同的:莱布尼茨所认为的曲线,是具有无穷小边长的无穷多边形,是静态的;而牛顿则认为曲线是动态的,代表了点的流动。牛顿和莱布尼茨都不可避免的遇到了无穷小量的定义问题,然而,这种即可以做除数又可以被忽略,像0又不是0的量,要到2个世纪之后才被严格定义。
尽管当时的符号系统尚不尽人意,但不可否认的是,笛卡尔,奥特雷德,莱布尼茨和牛顿的努力让数学符号在17世纪后半叶得以兴起,微积分的出现改变的数学、物理甚至整个世界的命运。
欧拉恒等式——指数和复数
符号在数学中的应用使得人们知道,某类数字的某类操作总是相似的。例如,如果设定 $x^2=a$,那么 $x=\sqrt{a}$,因而我们有 $(\sqrt{a})^2=a$。在符号出现之前,这看起来是不证自明的。但符号系统赋予我们对根号和指数新的理解,指数表示底数的连乘号,因此
\[(x^n)^m=\underbrace{x^n \times x^n \times...\times x^n}_m=x^{n \times m}\]因此 $(\sqrt{a})^2$ 可以被认为是 $a=a^{1/2\times{2}}=(a^{1/2})^2$。可以发现,根式不过指数为分数的一种写法。这种通过符号获得的认知是文字描述难以实现的。
符号不仅仅他所代表的数,还有它背后所蕴含的深刻含义,这也是为什么符号不仅仅是文字描述的简写,更是一种全新的思维模式的原因。历史上相当长的一段时间 $\sqrt{-1}$ 都困扰着数学研究者,这不仅仅是它作为 $x^2=-1$ 的解的意义,还有它作为一个数是否服从其他运算法则的问题。欧拉都不可避免的犯过类似 $\sqrt{-2}\cdot\sqrt{-3}=\sqrt{6}$ 的错误。因此虚数符号 $i$ 的引入,不仅仅是代替 $\sqrt{-1}$,它表示了一种前所未有的数的操作方式,即把数轴在平面上以原点为中心旋转 $90^{\circ}$。
18世纪的数学符号在经历了200多年的蓬勃发展之后终于趋近完美,欧拉观察到虚数的旋转特性,自然对数以及三角函数的周期性之间的微妙关系,从而发表了著名的欧拉恒等式。
\[e^{i\pi}+1=0\]在这个等式中,$e^{…}$ 表示自然的增长,$i$ 表示这种增长是沿着切向的(旋转),$\pi$ 表示旋转了 $180^{\circ}$,也就是说,对一个单位长度,旋转 $180^{\circ}$ 得到的长度就是原长度的相反值(和为0)。欧拉公式被誉为最优美的数学公式之一,反映了数学符号系统背后所对应的人们对真实世界的抽象理解。
结语
19世纪的哲学家淮海特说,一个好的记法可以把大脑从所有不必要的工作中解放出来,让大脑专注于更高深的问题。数学符号正是这样改变了人类的思考方式,让人类思维上升到了新的高度。表面上看来,数学似乎是根据一些运算法则来进行符号运算的技术,我们甚至不会察觉到,这些有助于一般化、统合性及更深层理解的思维,全部直接来自记法本身。现代社会中所有的技术,包括但不限于建筑、天文学、火炮技术、木匠技术、地图学、天体力学、化学、土木工程、时钟设计、流体动力学、流体静力学、磁力学、材料科学、音乐、航海学、光学、气体力学、造船和热力学的发展,都依赖于数学符号系统的建立。
实际上,人们几乎从来不使用文字进行思考,思考时,文字都会转换成图像和符号在脑海里发生,在思考结束之前,文字都不会出现在意识里。正如叔本华写下的:
“思想被文字体现的时刻,它就会死亡。”
你可能也喜欢: