这本书是著名哲学家伊姆雷·拉卡托斯于20世纪60年代完成的一部探索数学史上新的发现产生过程的经典著作。这本书以对话的形式构成,虚构了教师和学生在课堂上关于多面体的欧拉示性数的讨论。在讨论中,作者形象地展现了数学史上对此问题进行研究探索的真实的历史图景,以此来挑战和批判以希尔伯特为代表的认为数学等同于形式公理的抽象、把数学哲学与数学史割裂开来的形式主义数学史观。此篇光辉论著的主要目的是要解决数学方法论的基本问题,以一种探索和发现的情境逻辑来代替形式主义和逻辑实证主义的抽象教条。正如拉卡托斯所说:
非形式、准经验的数学的发展,并不只靠逐步增加的毋庸置疑的定理的数目,而是靠以思辨与批评、证明与反驳之逻辑对最初猜想的持续不断的改进。

欧拉示性数
对于正多边形来说,顶点数(V)与边数(E)满足 V=E;对于多面体,其顶点数(V)与棱数(E)以及面数(F)似乎满足 V-E+F=2 的简单关系。这一关系最早由笛卡尔与1635年左右证明,但不为人知。欧拉在1750年独立证明了这个公式。后来,笛卡尔的工作被发现,此后这个公式也被称为欧拉-笛卡尔公式。
我们可以尝试简单的测试一下欧拉的猜想:对于四面体,四面体有四个顶点(V=4),六条棱(E=6)和四个面(F=4),所以 V-E+F=2;对于正方体(长方体),V=8,E=12,F=6,所以 V-E+F=2;对于正十二面体,V=20,E=30,F=12,所以 V-E+F=2。
事实上并不是所有的多面体都满足欧拉示性数为2的特征。我们需要一些规范来保证我们讨论的多面体符合欧拉猜想的要求。第一类反例可以通过对规范的定义避免。例如下面的三个例子。

最左边的示意图表示一类中间有空洞的多面体。其欧拉示性数 V-E+F=4。右边的两个多面体似乎是共棱和共顶点的两个四面体。为了排除这些异类,我们可以增加一些对多面体的定义。
定义一,多面体是一个由多边形系统组成的曲面(排除空心立方体)
定义二,多面体的每个棱上恰好有两个多边形相交
定义三,对于多面体上的任何两个多边形,存在一条不穿过任何顶点和棱的路线,可以从一个多边形内部到达另一个多边形内部(排除共棱,共顶点)
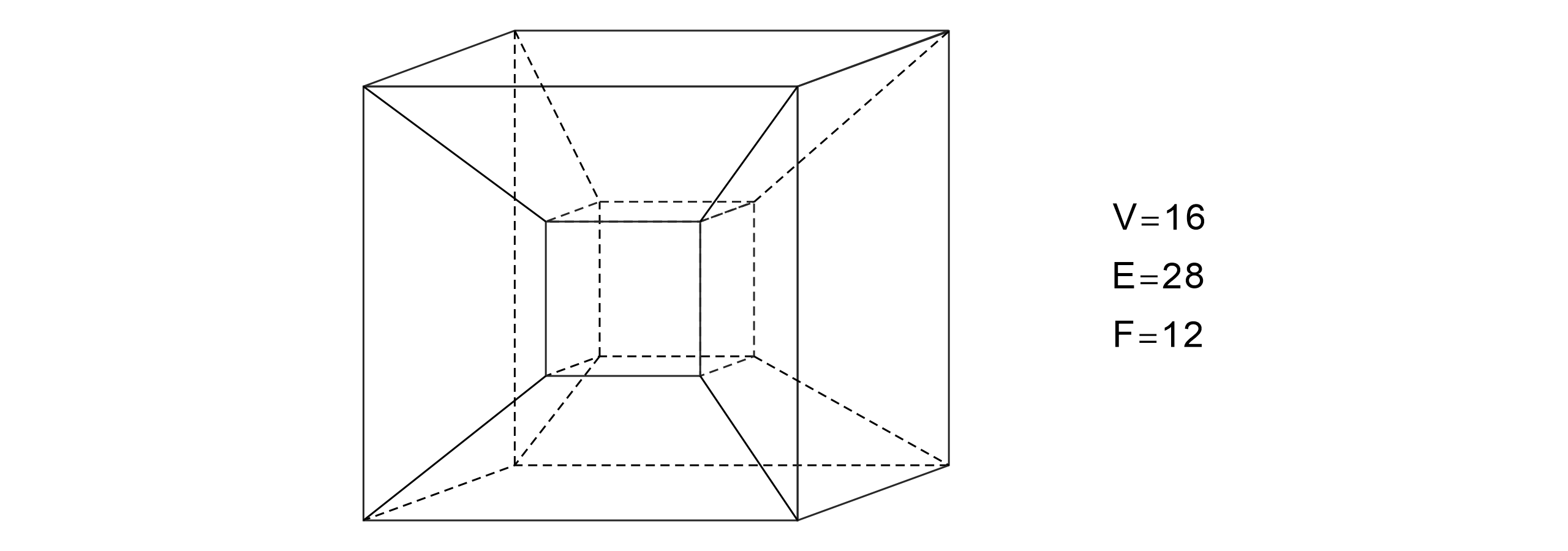
另外一个有趣的反例如下图所示,这个反例也被称为饰顶立方体,其欧拉示性数 V-E+F=3。
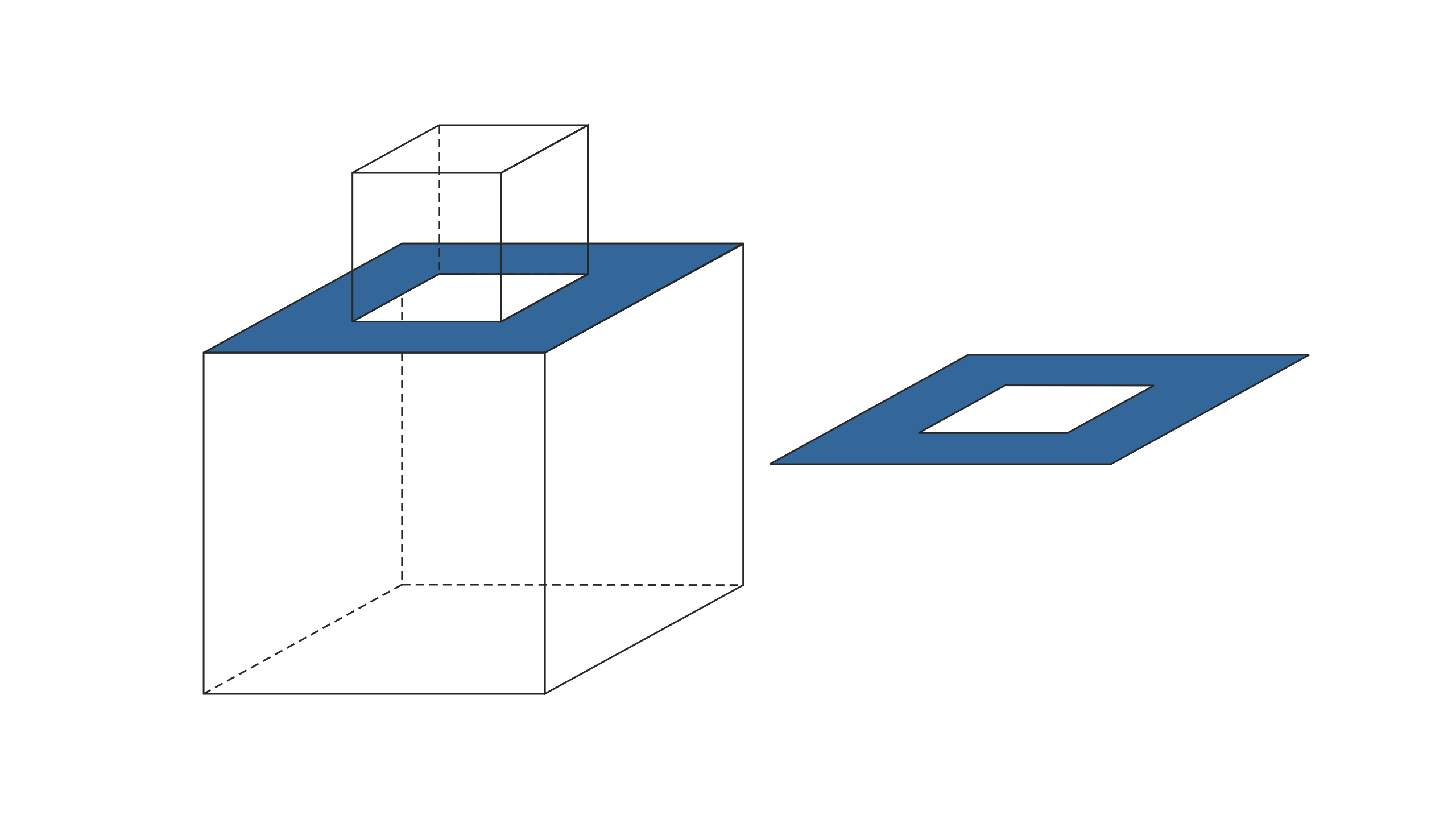
出现这一状况的原因在于饰顶多面体中出现了一个环状面,我们不妨增加一个定义:
定义四,构成多面体的多边形必须是单联通的。
即使这样,我们仍然可以举出反例——圆柱体。讲道理,圆柱体应该不能算是严格意义上的多面体,因为圆形并不能算是严格意义上的多边形,它甚至不符合多边形顶点数和边数相等(圆有一条边但没有顶点)。圆柱的欧拉示性数V-E+F=1。我们仍然可以通过补充定义的方法来解决这个问题:
定义五,棱有两个顶点。
排除异己是修正猜想正确的一个重要手段,在不破坏猜想本质的情况下,我们总是可以通过补充和准确定义的方式来为猜想划定范围,从而保证一个有意义的猜想不会被奇怪的反例所淹没。
次佳反例
下面要说道的反例是我在正本书中第二喜欢的反例。这个被成为开普勒星状体的多面体由十二个五角星组成,从某种意义上来说,它具有十二个顶点,三十条棱和十二个五角星面,其欧拉示性数为 V-E+F=-6。

如果认为五角星是一个具有五条边和五个顶点的多边形,那么星状体确实不符合欧拉猜想,但事实上,星状体也可以被看成是由60个三角形组成的多面体,它具有三十二个顶点,九十条棱和六十个面,因此 V-E+F=2!
事实上并不需要将星状体排除在欧拉多面体之外,我们需要的,仅仅是在用五角星构成的多面体中区分原来不独立的顶点和面。
定义六,每个顶点上恰好有两个棱相交(星状多边形嵌入到多面体后,来自不同多边形的棱相交构成了新的顶点,原来的五角星状多边形被划分为五个不同的三角形)
对欧拉公式的拓展
我们始终逃不开关于拓扑同源的讨论。试着数数下图中左边隧道多面体, 不难发现其欧拉示性数V-E+F=2。
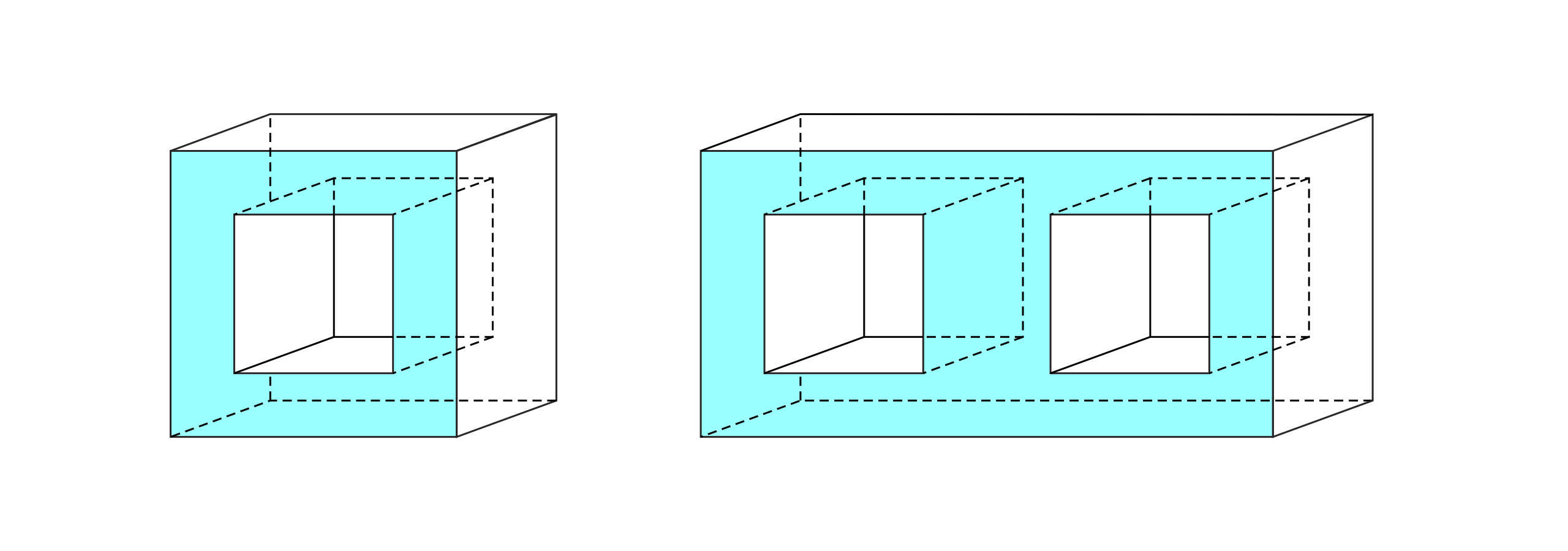
当然隧道多面体不满足定义四,它有两个面都不是单联通的,但隧道多面体本身的性质却值得讨论。欧拉示性数是一个拓扑不变量,对于一个球面同胚(Sphere)的多面体,欧拉示性数总是2。对于多联通的多面体,比如说环(Torus)同胚的多面体(在满足上面定义的前提下,i.e. 每个面都是单联通的),其欧拉示性数总是0。例如下图中的画框多面体,其环状面由4个梯形组成,由于没有多联通的面,则这个环状同胚的多面体欧拉示性数为0。
如果还记得上面提到的饰顶立方体,其欧拉示性数为3,我们可以做出如下的猜想,每个环状面(双联通面)可以提供+1的欧拉示性数,而每个环状的同胚结构将提供-2的欧拉示性数。因此隧道多面体总是有2的欧拉示性数,因为多面体每增加一个隧道(多一个环),就会增加两个双联通面。例如,隧道多面体右边那个有两个隧道的多面体,它有二十四个顶点,三十六条棱和十四个面,其欧拉示性数仍然为2。
柯西的证明
柯西为满足定义一至定义六的多面体给出了一个较为严格的证明,证明如下,
第一步,对于一个球状同胚的多面体,我们可以去掉它的一个面,并将剩下的面拉伸并平铺在一个平面上。如果我们对一个立方体进行操作(如下图所示),在去掉A面之后,剩下的面可以平铺在平面上。由于我们去掉了多面体的一个面,但并没有减少顶点和棱的个数,那么剩余结构的欧拉示性数应该为1。
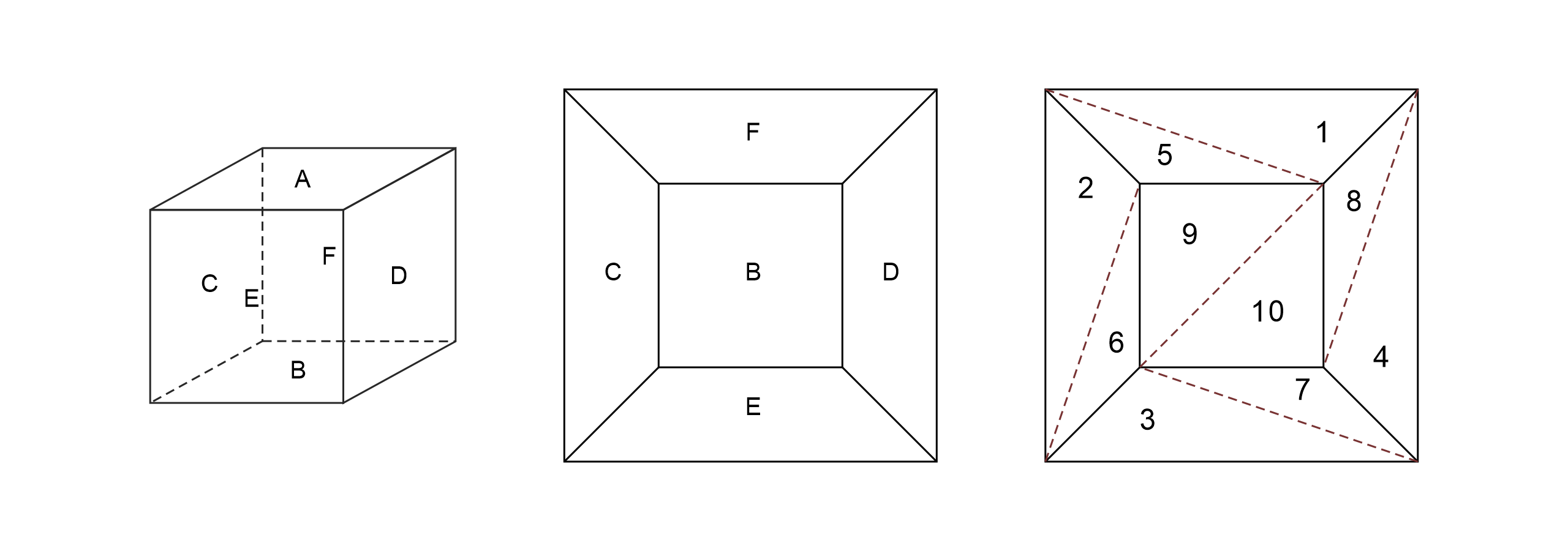
第二步,对于平铺在平面上的每个多边形,我们可以画对角线将多边形分割成多个三角形。(由于多面体的每个面都是单联通的,平铺之后也必须是单联通的,注意,这就是为什么必须要排除圆柱的原因,圆柱去掉顶面后平铺会得到一个环,不符合这一证明。)在划分三角形的过程中,每增加一条线段(棱),就会将原来的一个面分割成两个面,即增加了一个面,同时并没有顶点增加,因此欧拉示性数在这一操作中保持不变。
第三步,按照一定的步骤移除这些三角形,首先移除1-4,移除这四个三角形时,每移除一个三角形,减少一个面的同时减少一条棱,并且顶点数保持不变,因此欧拉示性数保持不变。然后按顺序移除5-9,这时每移除一个三角形,就减少一个面,同时减少两条棱和一个顶点,因此欧拉示性数仍然保持不变。最终将只剩下一个三角形。
对于最后的三角形,它拥有三个顶点,三个棱和一个面,其欧拉示性数为1,因此原多面体的欧拉示性数为2。值得注意的是,在这个证明中,平铺,切割和按照一定的顺序移除三角形都是十分重要的。
超越证明的反例
关于欧拉示性数的研究不会止步于此,在这本书中,这是我最喜欢的反例,它拥有 V-E+F=2 的多面体性质,却不能用柯西的方法进行证明。
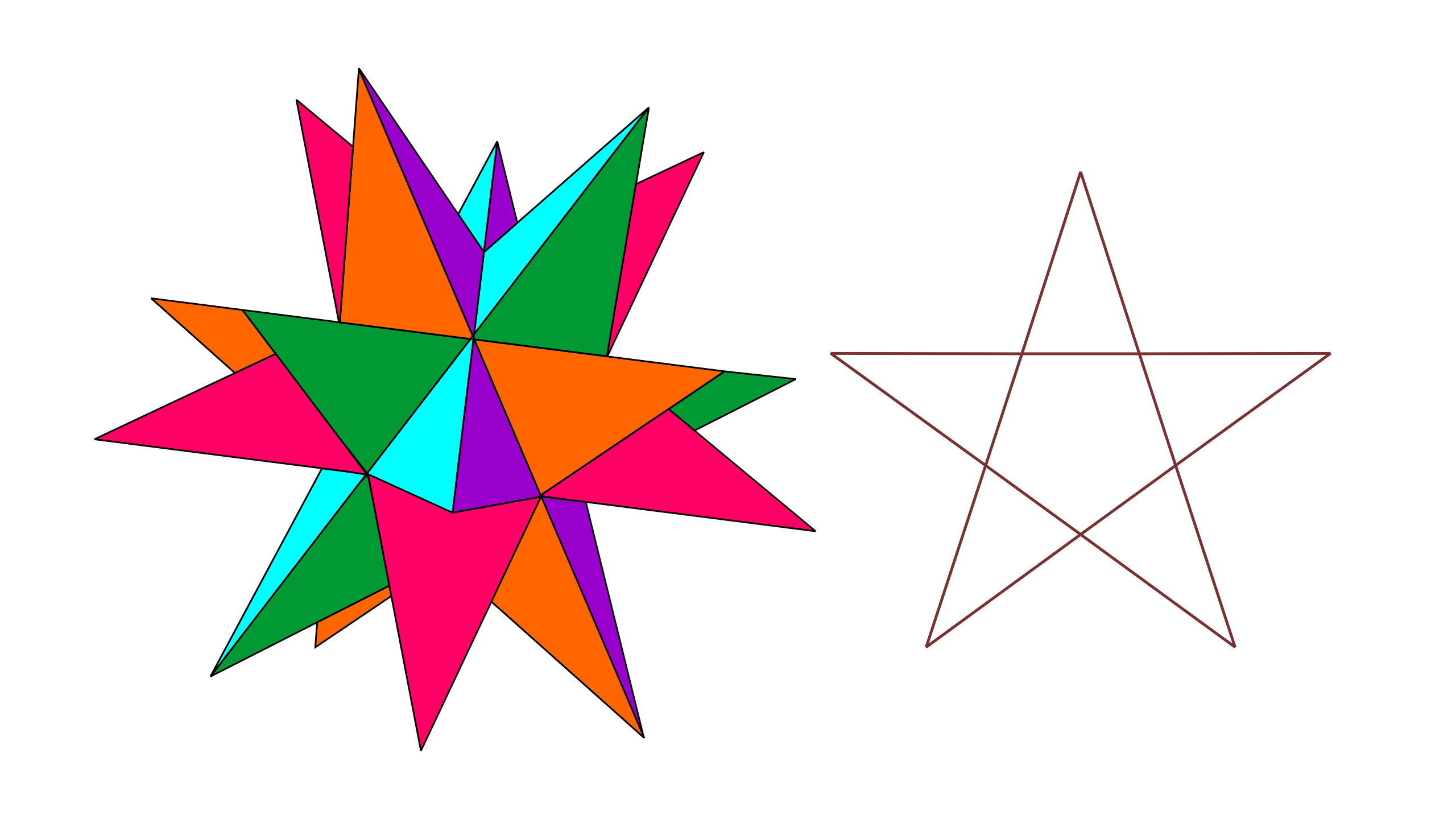
这个被称为大星状多面体的结构由12个五角星面按照和开普勒星状体不同的方式组合而成。它有20个顶点,30个棱和12个面,因此欧拉示性数为2 。当然柯西的证明也不能解释为什么隧道多面体拥有为2的欧拉示性数,在本书的后一部分,也有一些关于其他证明思路的讨论。
这本书旨在表明,数学发现并不是在基本公理上简单的逻辑推理演绎,而是在证明和反驳的过程中不断修正和完善的体系。哥德尔不完备定理指出,一个自洽的数学系统是不完备的,我们总是需要在讨论中增加更多的假设来修正我们的猜想。因此,即使如数学这样建立在公理体系上的逻辑学,也不是完全确定的,仍然有极大的未知等待探索。
你可能也喜欢:


