1669年,年仅27岁的艾萨克·牛顿被授予剑桥大学卢卡斯教授席位。据传闻,当时剑桥大学资金紧张,包括牛顿爵士在内的诸多教职工工资已经拖欠数月。为了解决这一问题,牛顿潜心研究并创立了微积分。从此,一门名叫“高等数学”的新科目成为了全校的必修课,并规定考试不及格者,来年必须缴费重修直至通过。很快教授们的工资就发下来了。
数学是一门抽象的艺术,它不像物理学——物理学是对现实世界的描述,数学是对想象世界的描述。在这个想象的世界里可以有完美的圆形,虽然现实世界中你没法握着一个真正的圆,但这不妨碍你在想象中测量它的面积和周长。
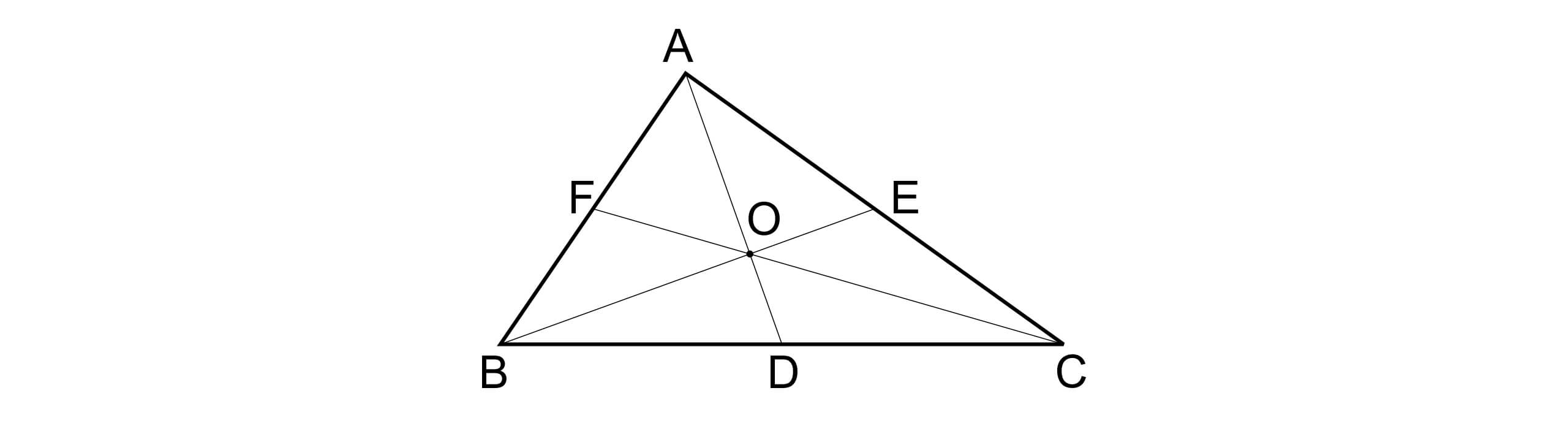
如果你不能很好的理解数学的奥义,不妨在脑海中想象一个三角形,然后连接三角形的三个顶点和它对边的中点,你可以已经注意到了,这三条线会交于一点。当然,你可以在纸上画出无数个不同的三角形,然后用显微镜仔细的观察这画在纸上的图形中三条线是否交于一点,但那是一个关于物理现实的科学问题。在这里,真正的秘密和纸笔无关,这一秘密是关于想象中的三角形的,这就是数学和物理的区别。我们不妨先放下三角形,先欣赏一番这里所说的想象世界的性质。
提示:超级超级长,不如直接翻到最后一段。
从平面几何到古典微积分
来想象一个边长为1的正方形,没有比这更简单的了。关于正方形有一个古老的问题:它的对角线长度是多少?
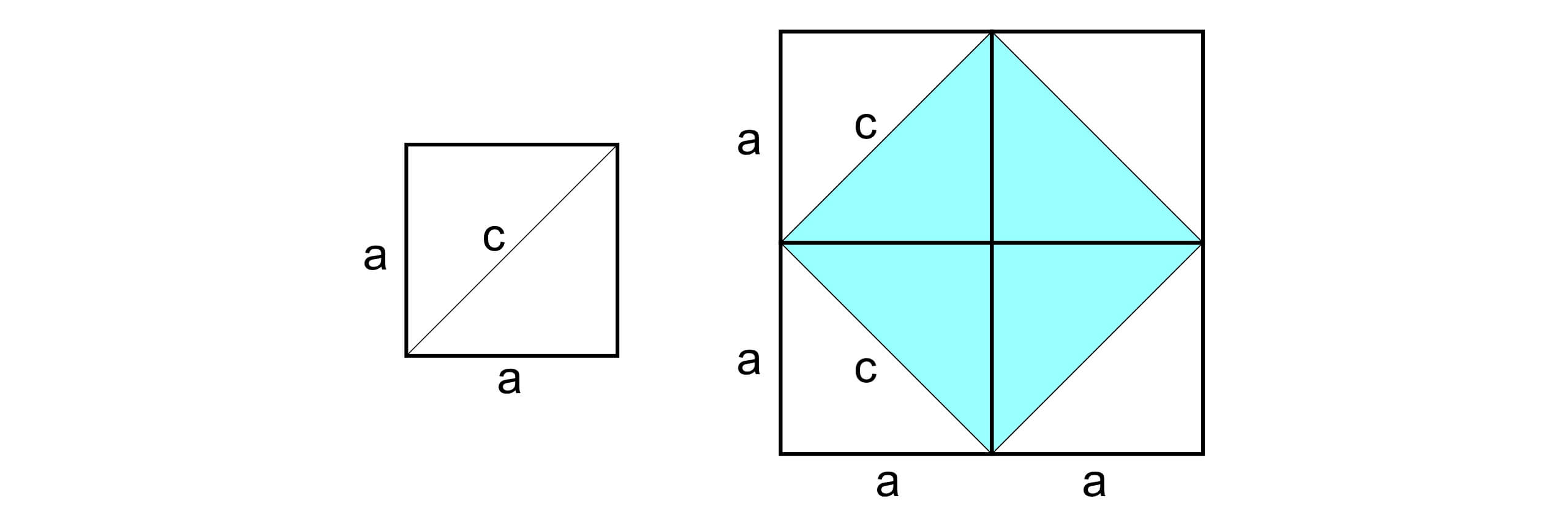
答案当然很简单,如同右边的图形所示,以正方形的对角线为边,恰好组成了一个面积为 2 的新正方形。我们可以先不讨论面积为 2 的正方形边长究竟有多长(当然这个关于无理数的话题也非常有趣),如果关注对角线长度 $c$ 和边长 $a$ 之间的关系,可以发现$c^2=2·a^2$。这可以看成是毕达哥拉斯定理的一个特殊形式。如果我们考虑一个矩形的对角线长度,如下图所示。
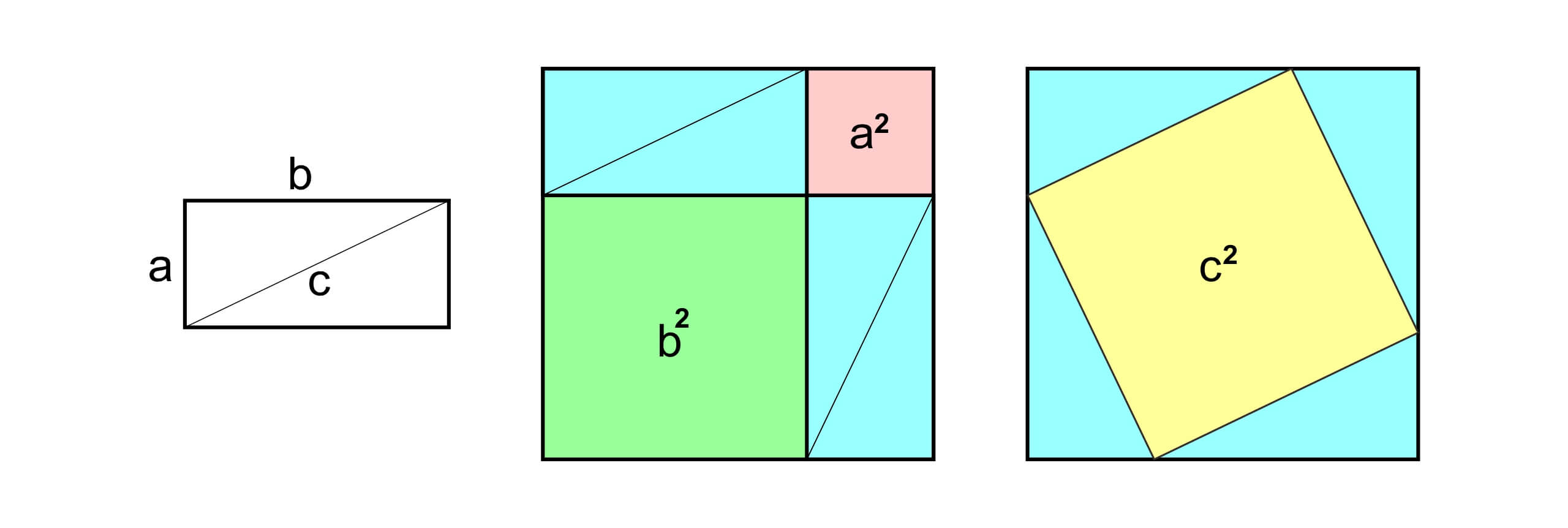
这个对毕达哥拉斯定理的证明和上面对正方形边长的求解有着异曲同工之妙。4000 年前人们就发现了矩形的对角线和边长之间的关系,但时至今日,这样的巧妙证明仍然让人叹为观止。
在明白了一些基本的技巧之后,我想我们可以试试一些更有趣的图形——五边形的对角线长度是多少。
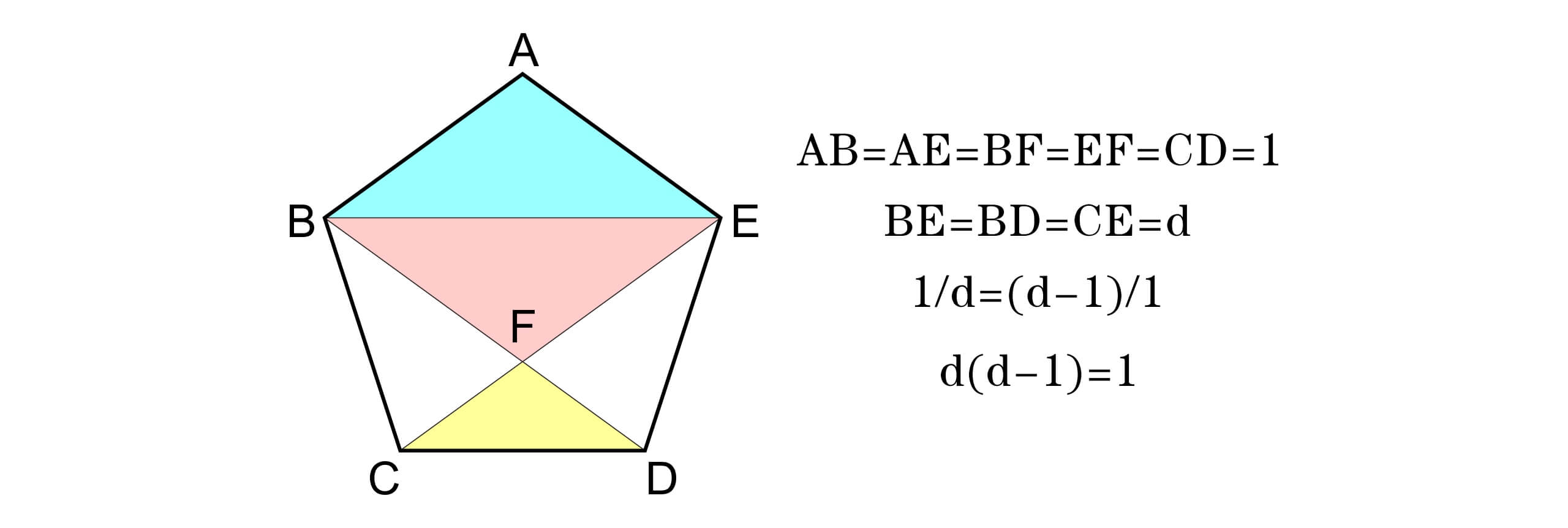
画出几条对角线之后,我们可以发现三角形ABE与三角形 BFE 全等,而三角形 BFE 与三角形 CFD 相似。假设五边形的边长为 1 ,对角线长为 $d$。则不难发现五边形的边长和对角线长满足:$1/d=(d-1)/1$。或者说:$d\cdot(d-1)=1$。按照代数的方式来求解这样的方程虽然已经很简单,但通过几何的描述可以更容易的发现规律背后的美感。
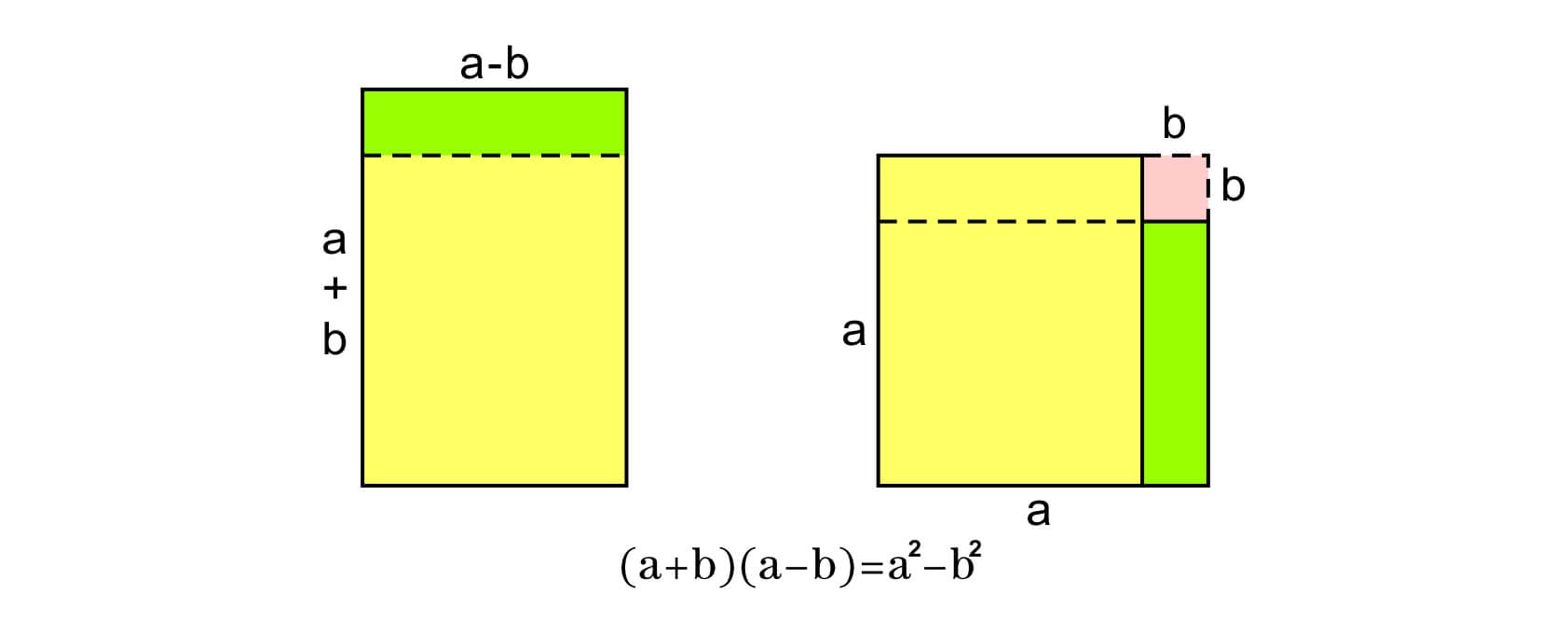
在这个考虑中我们不妨把一个长方形的长边和短边分别表示为 $(a+b)$ 和 $(a-b)$ 。它们的乘积也就是长方形的面积可以表示为两个正方形面积之差 $(a+b)(a-b)=a^2-b^2$。因此 $d(d-1)=1$ 也可以表示成 $(d+1/2)^2-1/4=1$。不难发现五边形的对角线长与边长之比d就恰好是黄金比例。这也是五边形如此迷人的原因。在传统的几何中, 面积和长度都可以通过切割和拼接来表示。而无穷分割就是古典微积分方法的精髓。 如果要求一个圆形的面积,不妨沿着半径把圆切割正无穷多个三角形,这些三角形的高都是圆的半径r,这些三角形的底边长之和恰好是圆的周长 $S$。因此圆的面积也可以表示为 $r\cdot C/2$。
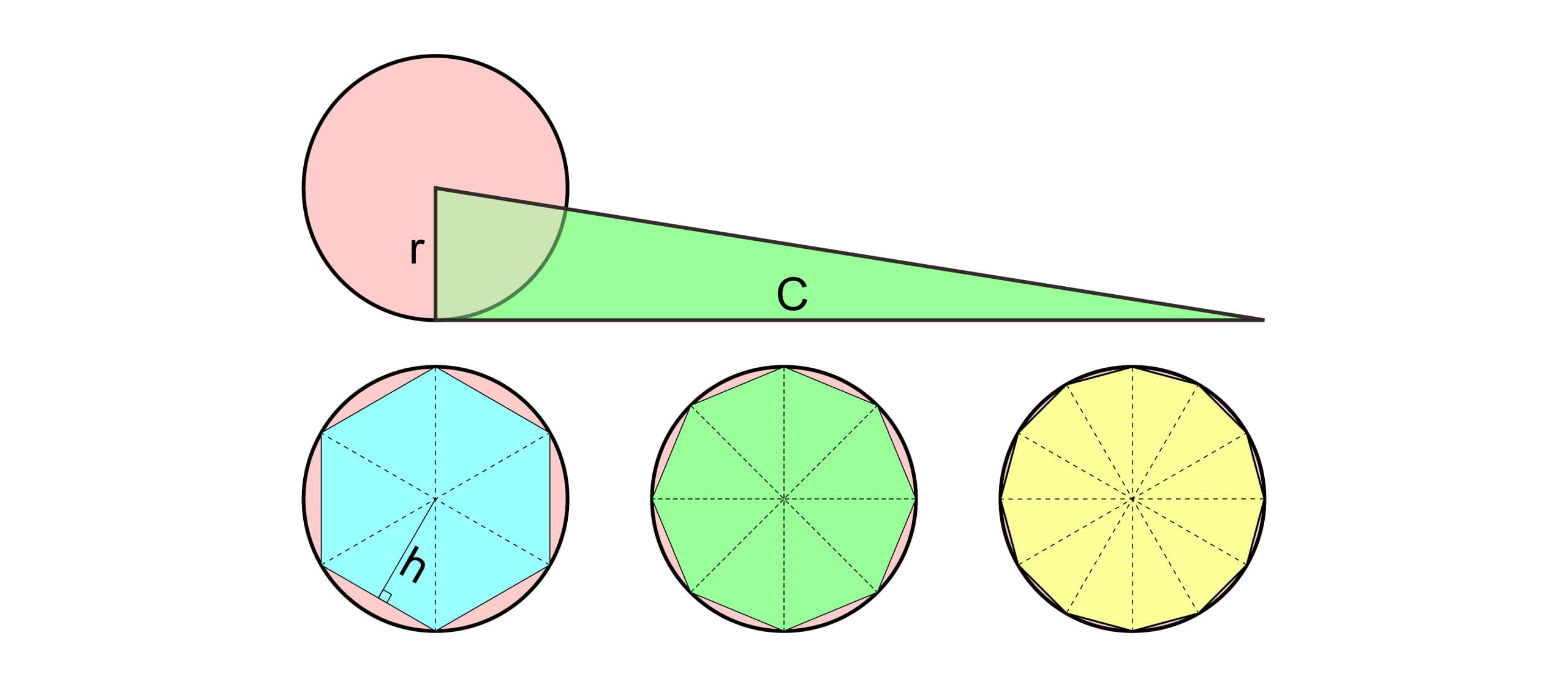
求解圆的周长则和面积相似,在圆的内切正多边形中,随着边数的增加,多边形的周长逐渐逼近圆的周长。很不幸的,圆的周长与直径之比π是一个超越数,这意味着我们只能用增加多边形边数的方法来逼近圆周长,却不能用一个长度来直接表示圆周长。
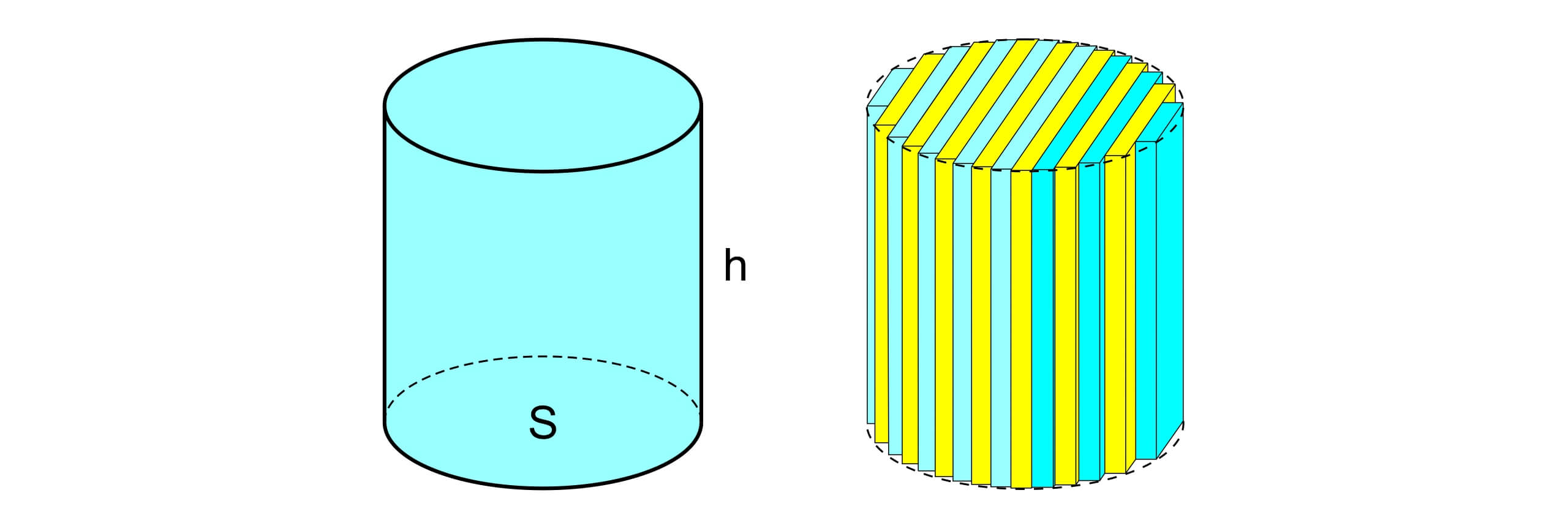
对体积的讨论也可以通过无穷分割方法转换成立方体体积的叠加。圆柱是一个最简单的例子,当把圆柱切割成无穷多个无限薄的长方体后,可以发现,圆柱的体积和这些长方体的体积之和一样,并且可以写做圆柱底面积 $S$ 和高 $h$ 的乘积。
如果要计算一个锥体的体积,无穷切割的办法可能就比较困难。但如果考虑一个在正方体内的四棱锥,我们可以发现,因为一个正方体有六个面,图中的四棱锥恰好占有正方体体积的 $1/6$,或者说一个四棱锥的体积恰好是和它同底等高的长方体体积的 $1/3$。
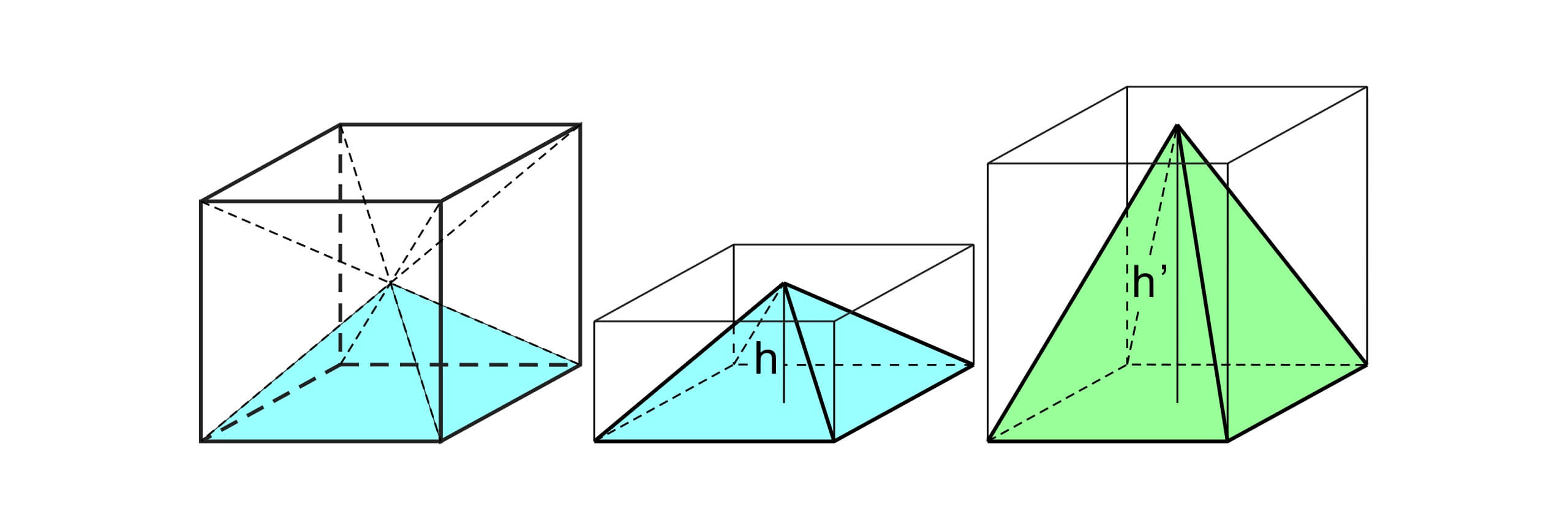
这一性质在沿着四棱锥高的方向对它进行拉伸以后依然不变。当我们考虑一个和棱锥有着相同底面积和相同高度的圆锥时,它们的体积是否也一样呢?如果考虑切掉两个椎体最底下的一个薄层,因为棱锥和圆锥有着相同的底面积,那么这个薄层的体积也应该相同。对于棱锥和圆锥剩下的部分,我们可以认为那是一个缩小版的棱锥和圆锥。如果把这个缩小版的锥体按照高度放大成为原来的锥体,可以惊喜的发现,放大后的棱锥和圆锥有着相同的底面积。这意味着,被切掉一层的棱锥和圆锥仍然有着相同的底面积。如果我们重复这个操作,可以意识到,圆锥的体积和拥有相同底面积的棱锥的体积一样,更重要的,它也是拥有相同底面的圆柱体积的 $1/3$。
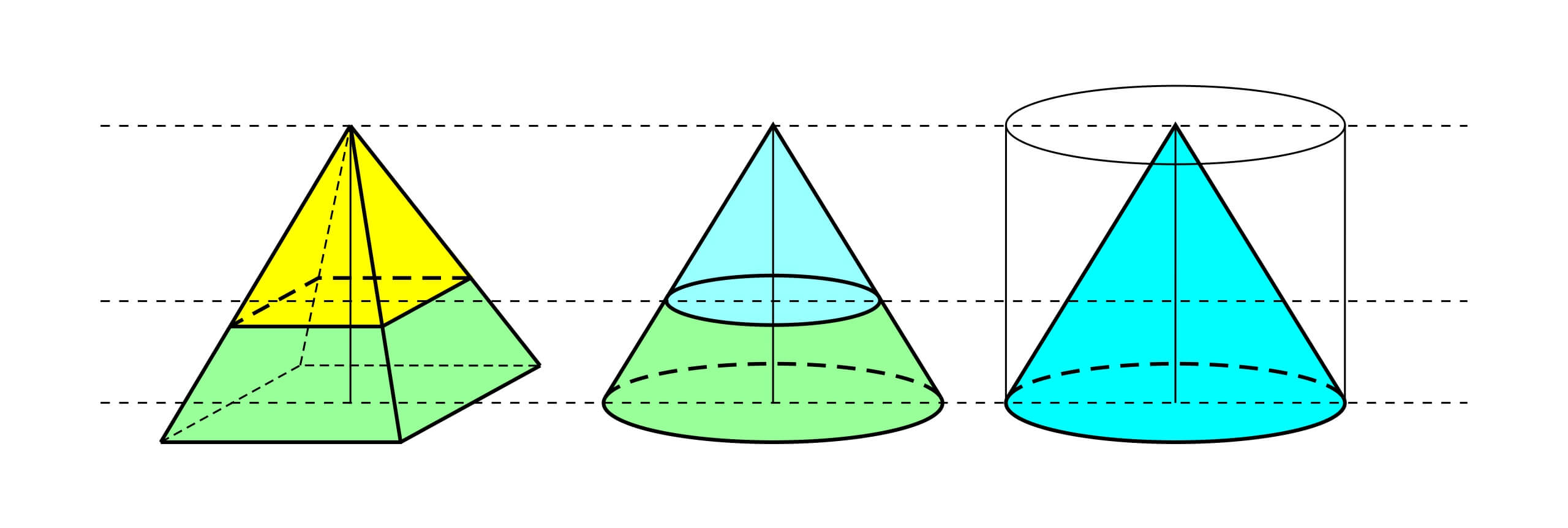
这个证明告诉我们,如果两个立体的每个平行截面都拥有相同的面积,那么他们的体积也相等。如果我们想计算一个立体的体积,比如说球体,我们可以尝试找到一个和球的截面相等的立体图形。
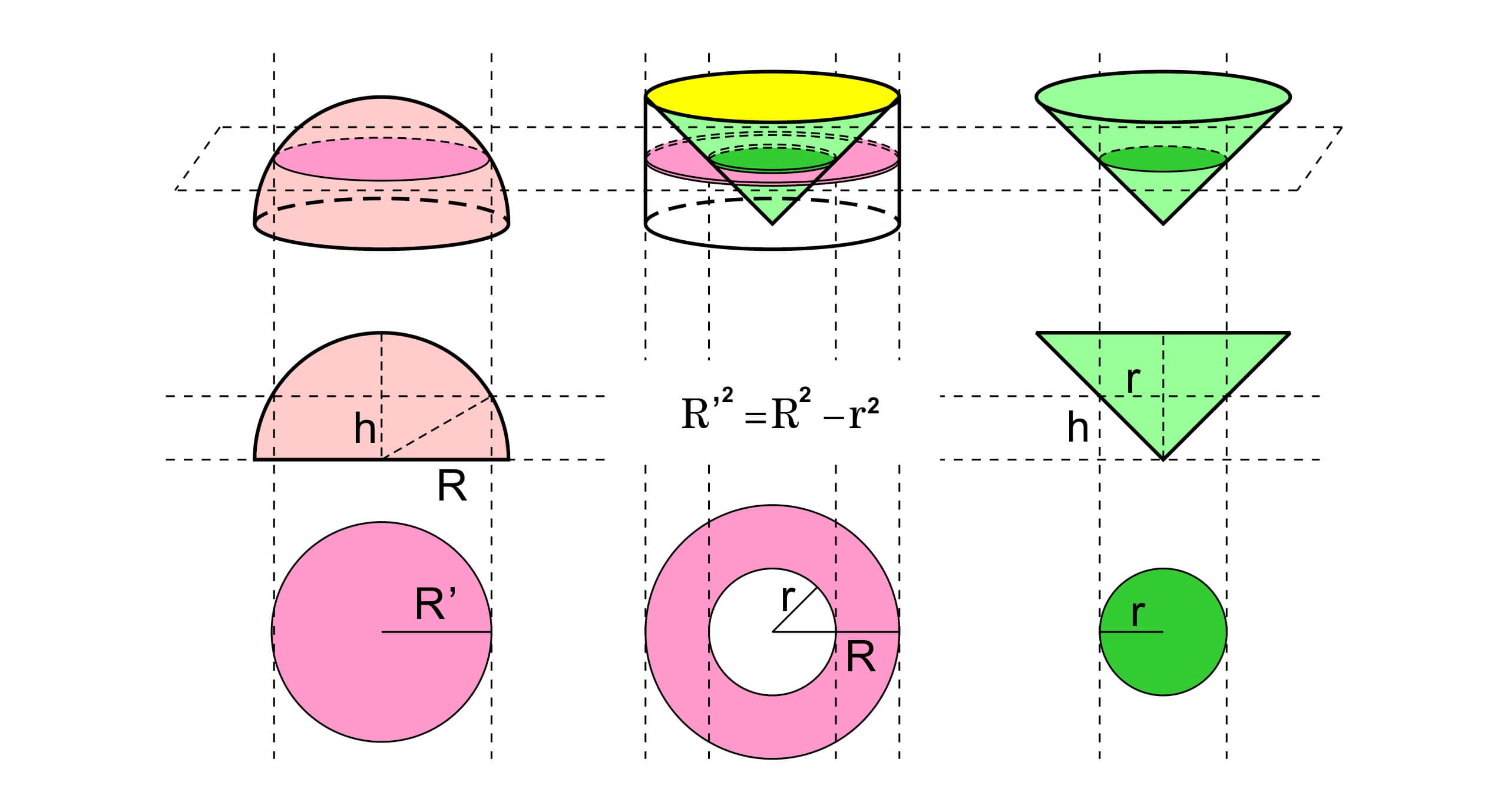
如图所示的球的截面恰好可以写成一个环形的形式,根据毕达哥拉斯定理,这个环形的内圆恰好是一个同底等高的倒圆锥在同样高度的截面。这意味着,一个半球的体积恰好是一个圆柱的体积减去圆锥体积剩下的部分。考虑到这个圆柱的高和底面圆的半径同为R,则半球的体积恰好为 $2\pi R^3/3$,因此球的体积为 $4\pi R^3/3$。公元五世纪,祖冲之和他的儿子祖暅利用这一方法首次计算出了球体的体积,虽然没有严格证明,但无疑是古典微积分的。
如果要计算球体的表面积(这一过程相当复杂,因为球面的高斯曲率不为0,因此不能展开到一个平面上),我们可以考虑球面由无穷多的——比如说三角形——铺满,而整个球体的体积则和这些三棱锥的体积相等。我们知道考虑这些三棱锥的高都为R,则他们的体积为和同底等高的立方体的 $1/3$。因此整个球体的体积可以表示为球的表面积S与半径R乘积的1/3。我们刚才已经计算过球体的体积,所以表面积 $S=3V/R=4\pi R^2$。

数学思想中的简化就是把未知的问题简化为已知的问题,在古典微积分中,我们把曲线看成是无穷多的直线(段)的组合,把曲面看成是无穷多的平面的组合。在对直线段和平面组成的面积和体积的度量基础上,实现对曲线和曲面性质的测量。
现代微积分
将数字和图像结合的经典范例应该算是数轴的引入。在数轴上,每个点都对应一个数字,数轴是连续的,这些数字也是连续的。我们对平面和空间的理解,可以用在正交数轴中的点来表示。这样一来,每一个几何图形都可以用一组坐标来表示。
如果考虑一个在一维空间内运动的物体,它的运动可以用两个独立的数轴来描述,其中一个描述时间的流逝,另一个则描述它所处的位置。每一个在时间轴上的点,都有一个在坐标轴(x轴)上对应的点。这种对应关系(函数)可以在一个直角化的坐标系中用一条曲线来表述。
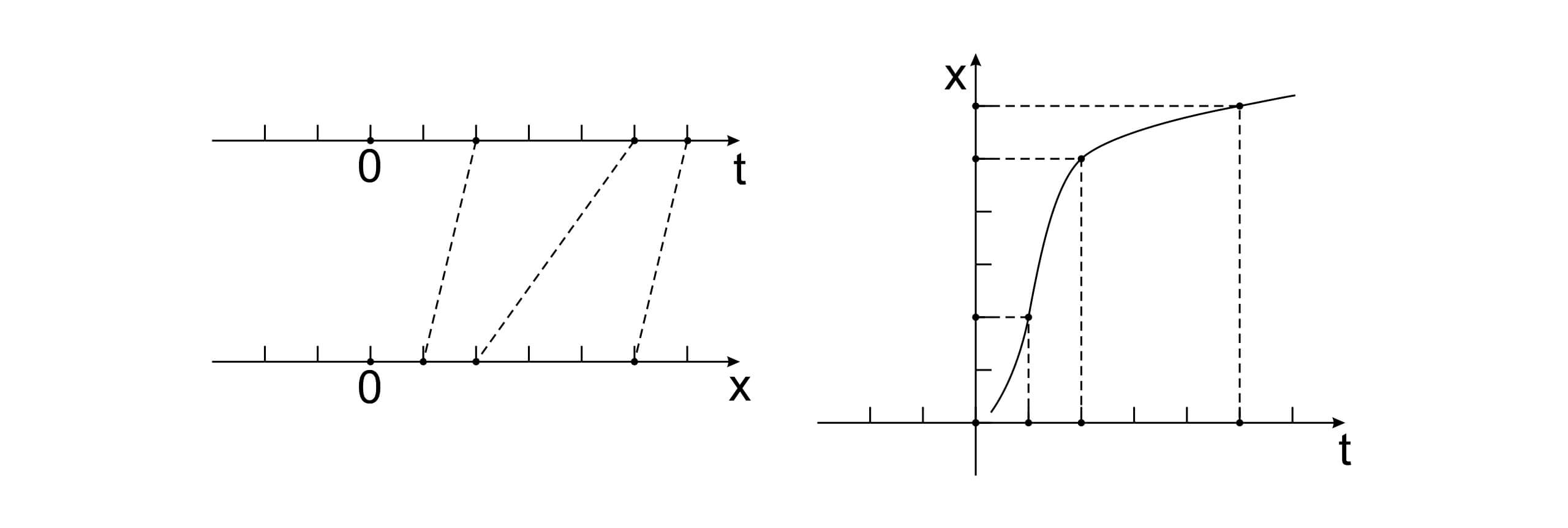
如果考虑在一维空间上的匀速直线运动,那么它的“位置-时间”图也是一条直线。更重要的,我们可以发现这条直线的斜率就是运动的速度。这不是巧合,因为速度的定义就是在单位时间内的坐标变化。但如果我们想要测量一个复杂运动的速度,那么在一段时间($\Delta t$)内的坐标变化($\Delta x$)就可能不再是固定不变的。
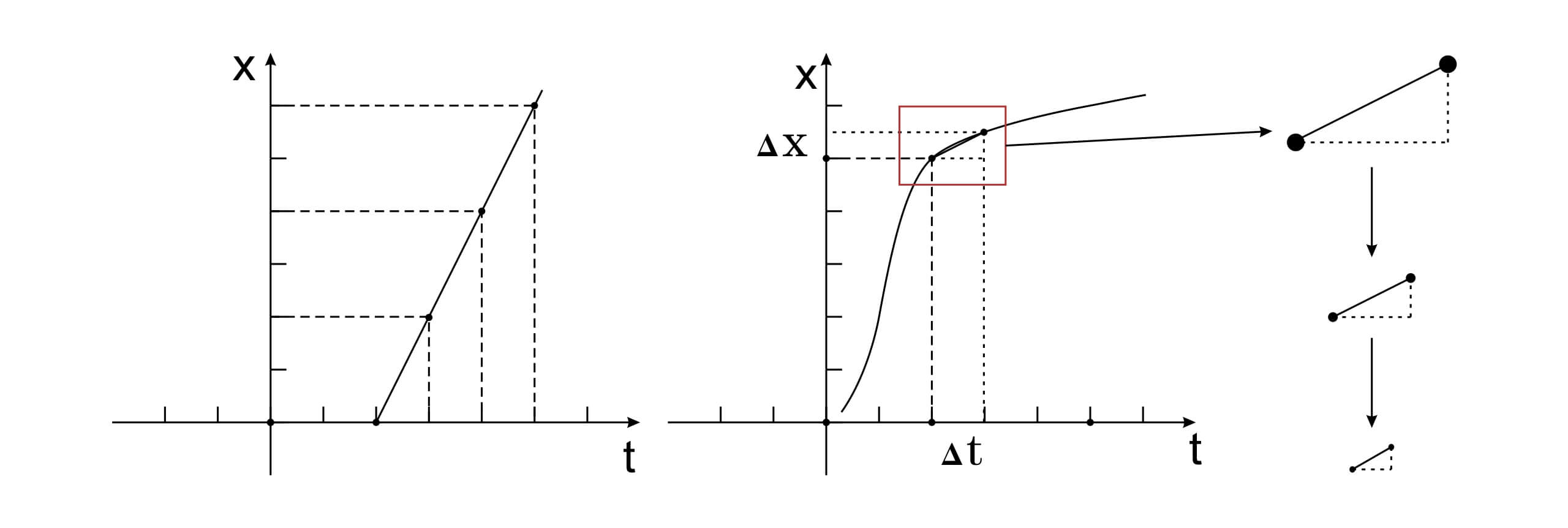
现代微积分的核心就是引入了无穷小的概念。注意:无穷小量即不是 0,也不是一个确定的数值,无穷小描述的是一个趋近与 0 的无穷序列。在这个序列中,1. 每一项都大于 0,2. 后一项比前一项更小。对无穷小这个极限的描述成就了对曲线斜率的定义,即当 $\Delta t$ 为无穷小时 $\Delta x/\Delta t$ 的值就是曲线的斜率。
在古典微积分时代,微分和积分被视为是独立的学科,由于没有系统的计算微分和积分的方法,无穷小的概念也难以获得认可。牛顿和莱布尼茨被认为是同时独立的澄清了微分和积分的关系,虽然也没能给出无穷小的精确定义,但他们给出了微积分的基本计算方法,并且将系统的微积分应用到几何与物理研究。
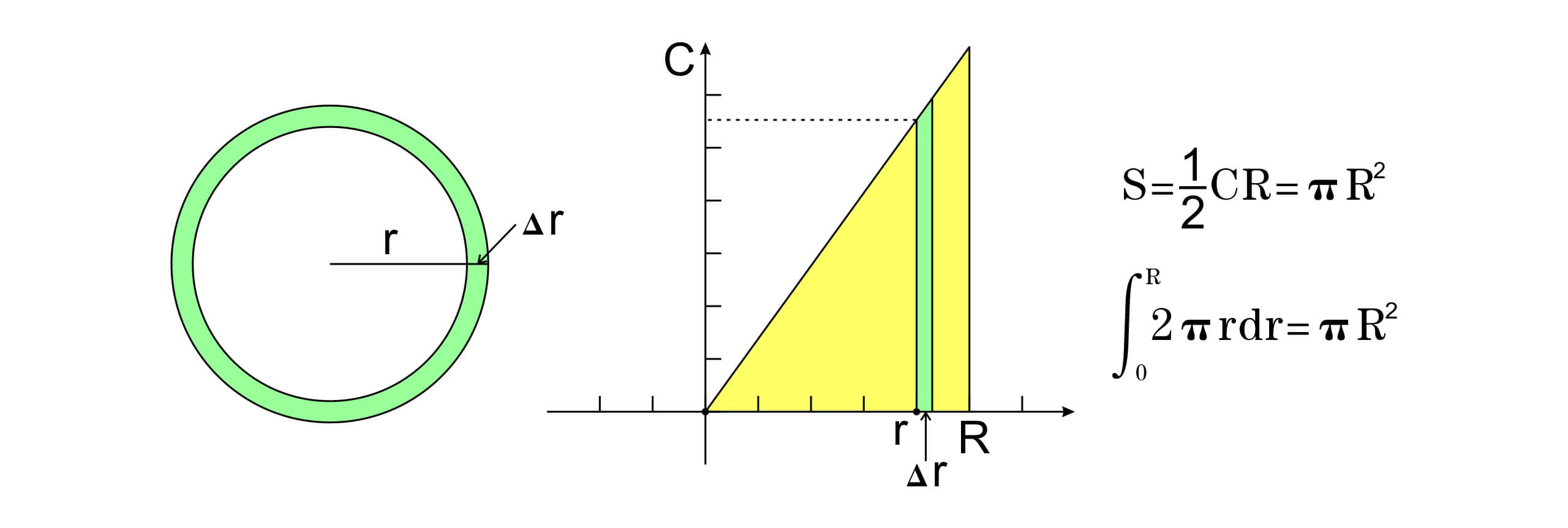
我们用圆的面积来完成对微分和积分的定义。考虑圆的面积 $S$ 和半径 $r$ 的关系,当 $r$ 增加一个无穷小量 $\Delta r$ 时,面积S的增长可以看成是一个圆环的面积,甚至更简单的可以写为 $\Delta S=2\pi r\Delta r$。根据上面对微分的定义,如果我们做出圆的面积 $S$ 随半径 $r$ 变化的曲线,那么曲线的斜率在半径为 $r$ 的位置则为 $2\pi r$。积分的定义则恰好相反,如果我们写出斜率随半径变化的曲线 $2\pi r-r$,则圆的面积可以表示为这条曲线和横坐标r之间的面积,也就是对 $2\pi r\Delta r$的积分。积分的计算恰好是微分计算的反运算,因此 $S-r$ 曲线在每一点的斜率就构成了 $2\pi r-r$ 曲线,同时 $2\pi r-r$ 曲线的面积就是 $S-r$ 曲线。
微分学还有一个重要的应用就是描述变化,因为微分(或者说导数)是对曲线斜率的描述,我们知道当一条曲线由上升(斜率大于零)转变为下降(斜率小于零)的过程中,一定存在一个斜率为零的点,同时这个点也代表了这条曲线的局部最大值。
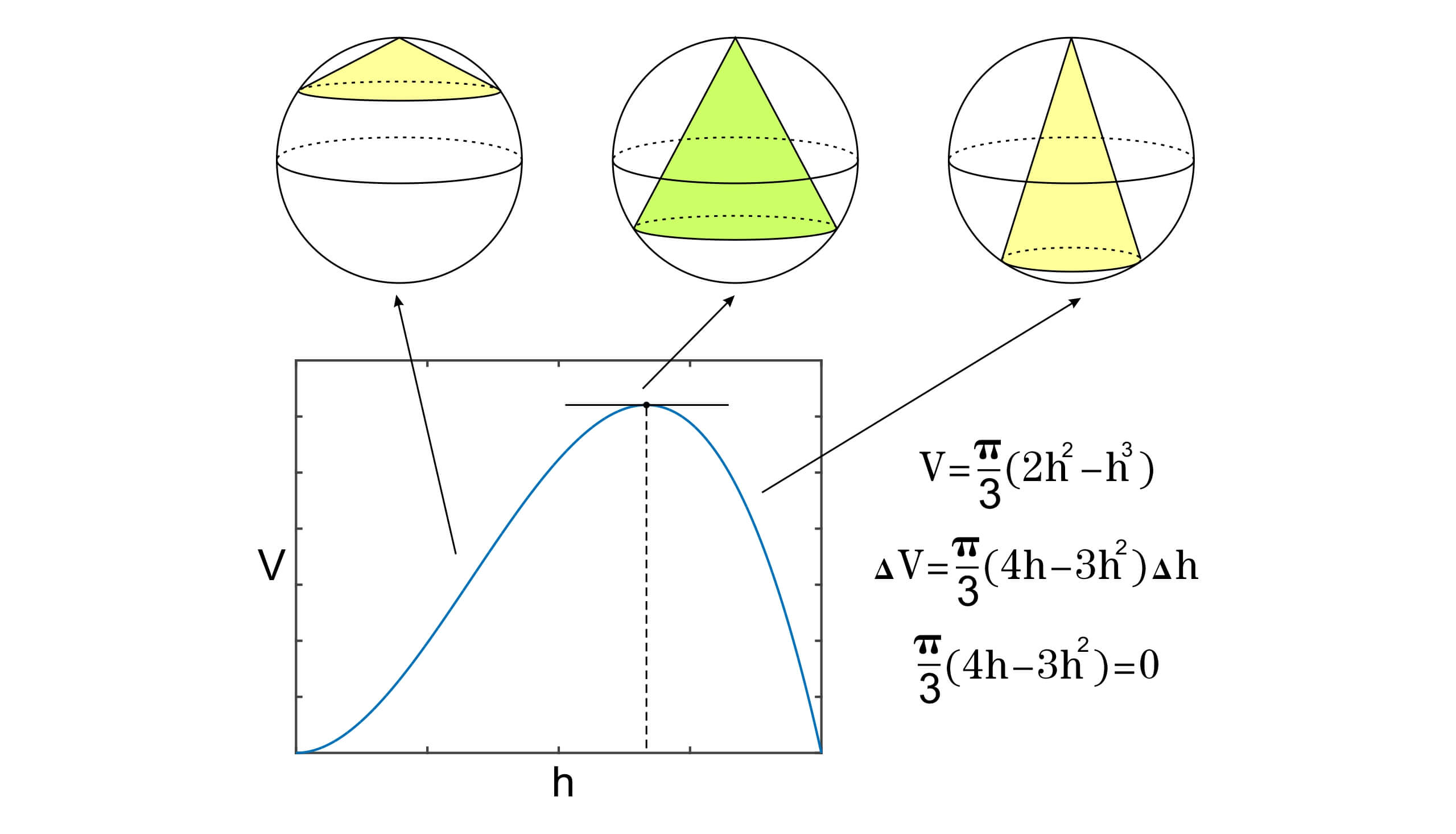
我们知道一个圆锥体的体积恰好是包围它的圆柱体积的 $1/3$,但如果我们在球体中画一个圆锥,我们可以发现,随着圆锥的高的变化,我们可以得到不同体积的圆锥。并且,当圆锥的高度由小变大时,它的体积会先变大然后再变小。那么球中所包围的圆锥体积最大为多少呢?我们可以写出圆锥体积V随高度h变化的关系 $V=\pi(2h^2-h^3)/3$。如果画出 $V-h$ 曲线,那么曲线上斜率由正变为负的过程中,斜率为 0 的点就应该是体积V的最大值。
现代分析学改写了古典微积分中的一些表述,在后来的发展中,由柯西给定的无穷小量的严格表述让分析数学成为了从逻辑上到符号上都严谨的逻辑科学。但微积分仍然在应用中有着不可分割的图像意义。
圆锥曲线和自然对数
我们都可以想象圆形在一个方向上拉伸变成椭圆形的情形,更一般的,拉伸变换也可以看成是一种投影变换。如果我们用一个平面去截一个圆柱体,那么截面就相当于圆柱底面在这个平面上的投影,因而也是一个椭圆。同样的情况在我们用一个平面去截一个圆锥体时也会发生。可能有人会觉得,圆锥的截面更可能是一个不那么对称的卵形,但这里有一个非常漂亮的证明。 我们知道椭圆有两个焦点,椭圆上的点到两个焦点的距离和保持不变。如果我们在圆锥和截面之间塞入两个球体,这两个球体刚好处于截面的两侧和截面相切,并且两个球的大小合适因而和圆锥面也相切(切线恰好为一个圆)。下面我们要证明,截面和球体的两个相切点 P, Q 为截面椭圆的焦点。
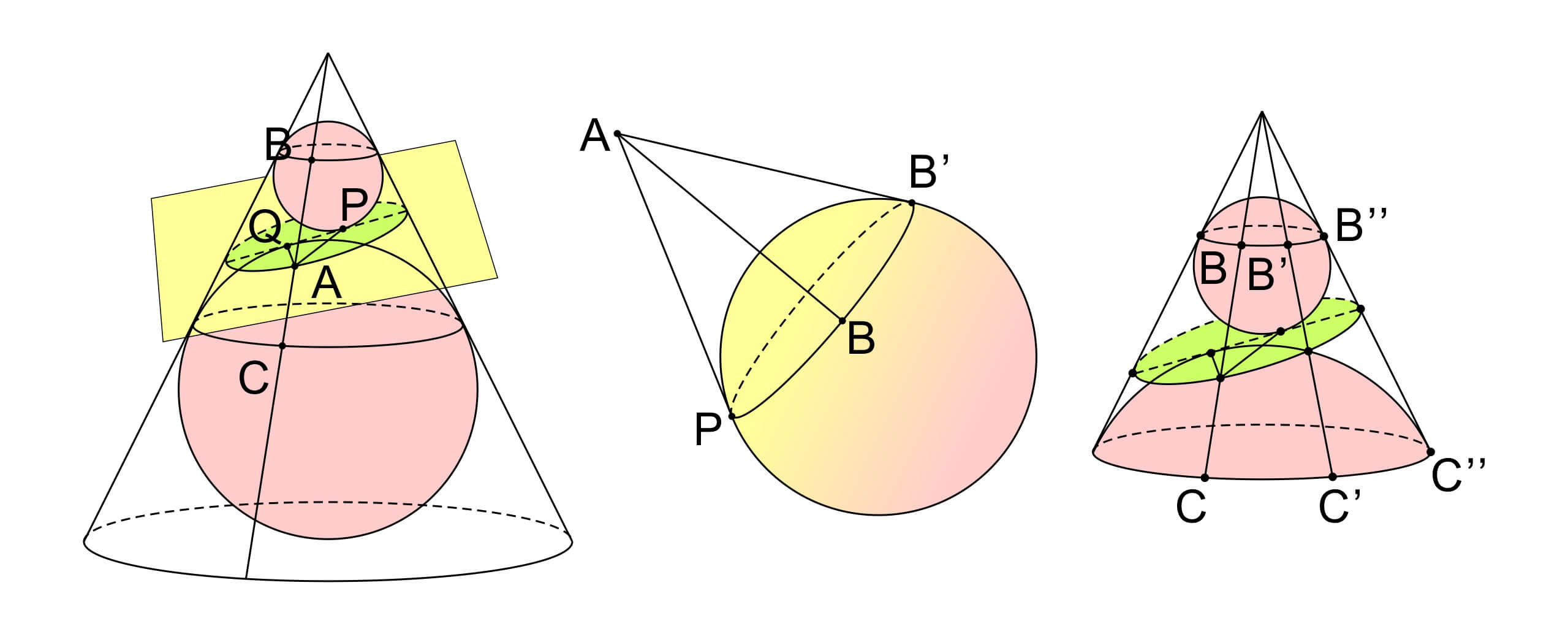
考虑椭圆上的一点 A,则 AP 为球的一条切线。考虑圆锥顶点与A的连线一定和球与圆锥的切线相交于一点 B,AB 也为球的一条切线。对于球外的一点,我们可以证明该点到球的所有切线都是等长的,因此 AB=AP。同理,我们可以得到 AC=AQ。考虑从顶点出发沿着圆锥面的线段在两个球与圆锥面切线之间的部分,我们可以发现这些线段都是等长的,即 BC=B’C’=B’‘C’‘。因此,对于椭圆上的任意一点,我们都有 AP+AQ=constant。
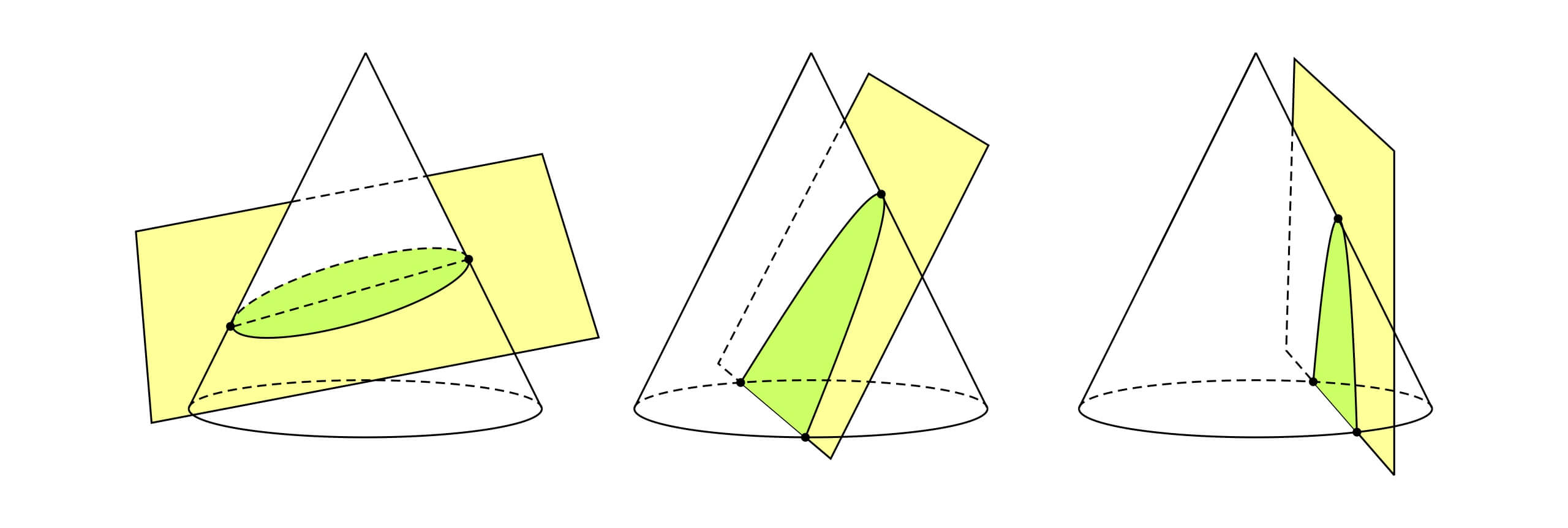
人们从公元前 200 年就开始研究圆锥曲线的性质,除了椭圆,如果我们继续倾斜截面直到截面和圆锥的外侧平行,那么截得的图形就不在闭合,从投影的角度来看,圆的一侧投影在了平面的无穷远处。这时得到的曲线为抛物线。如果我们继续倾斜截面,这时圆的一部分点就不会再投影到截面上,有趣的是,这部分点会投影在另外一侧。一个圆被投影到一个平面上的两条曲线上,这时的图形也被称为双曲线。双曲线的性质和椭圆恰好相反,双曲线上的点到两个焦点的距离之差为常数。
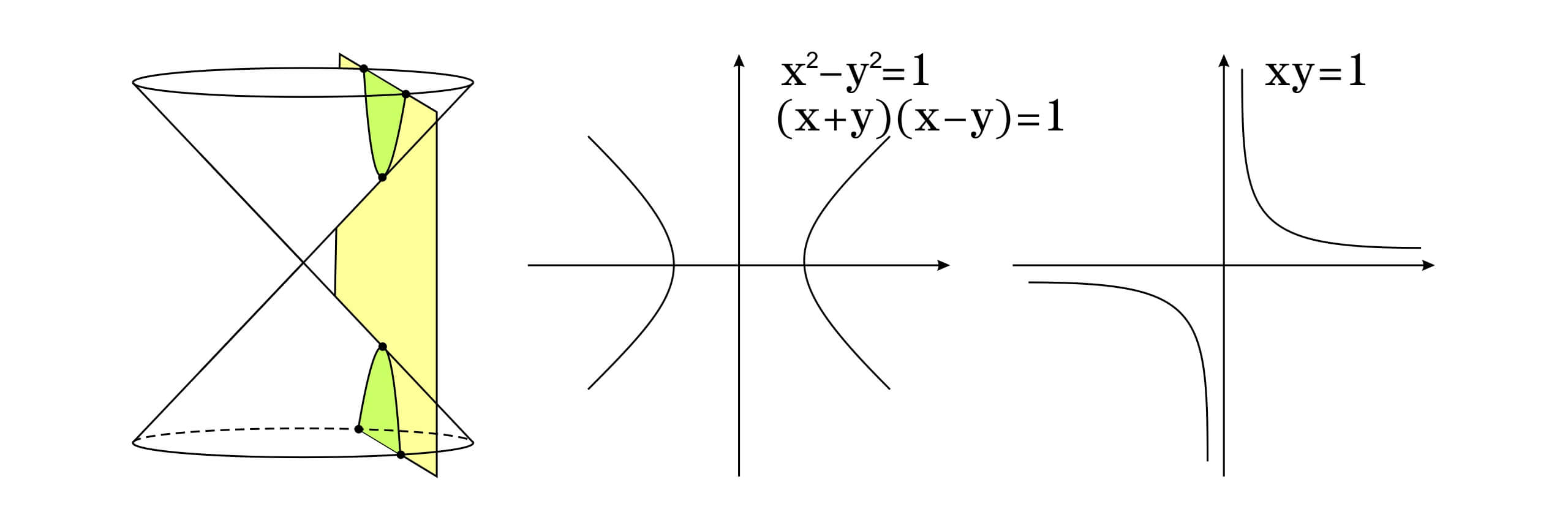
如果我们考虑一种最简单的双曲线,并且把它写成坐标形式 $x^2-y^2=1$。如果还没有忘记平方差公式,那么我们可以根据 $x^2-y^2=(x+y)(x-y)$ 把双曲线方程变为乘积模式,适当的换元之后我们可以发现,导数函数 $y=1/x$ 和双曲线是一样的。我们关注的重点不在于双曲线的各种变换有怎样的性质,而是希望通过间接的方程来描述更一般的问题。例如,倒数函数 $1/x$ 与坐标轴之间的面积,也就是 $dx/x$ 的积分拥有怎样的形式?
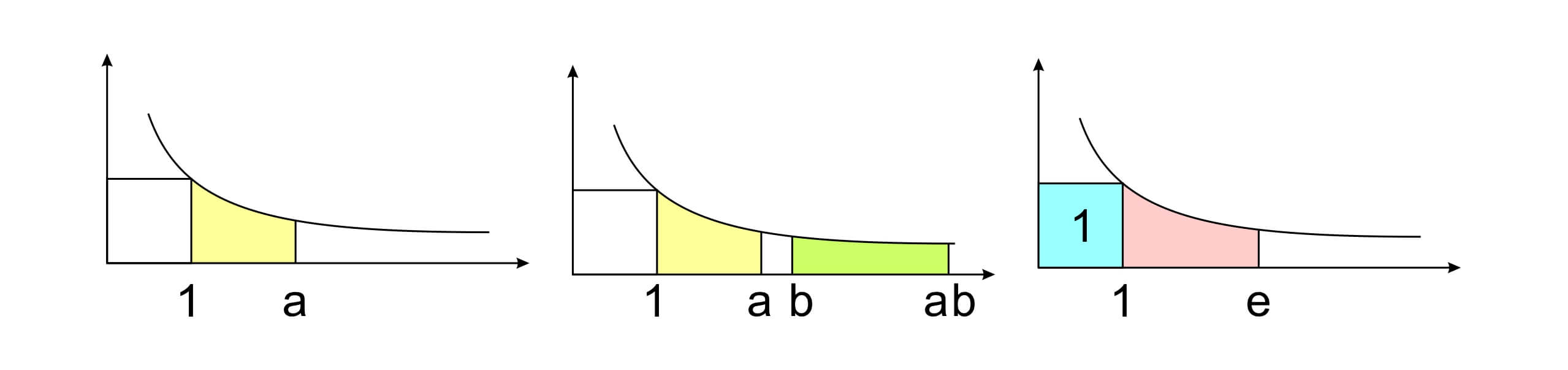
最简单的,我们考虑从 $x=1$ 到 $x=a$ 之间的面积,把它记为 $A(a)$。不难发现这一面积和 $x=b$ 到 $x=ab$ 之间的面积相等。注意:第二个区域的宽度是第一个区域的 $b$ 倍,而在任意位置,第二个区域的高度也是第一个区域的 $1/b$。因此我们可以得到,$A(a)=A(ab)-A(b)$,或者写成 $A(ab)=A(a)+A(b)$。
我们可以暂时放下这条奇特的性质,来回顾一下历史上做过同样事情的人。人们早就发现,乘法的计算相比加法计算复杂的多,那么有没有什么办法把乘法变成加法呢?约翰·纳皮尔在 1610 年发明了一种可以把乘法计算变成加法计算的方法。我们知道,任何数和 10 相乘就是在后面写 0 就可以了,当然这不是因为 10 很特殊,而是因为我们采用 十进制 来表示数。因此对于$10^5\times 10^4$这样的运算,其结果为 $10^{4+5}=10^9$。纳皮尔意识到,对于任意一个数,比如 32768,一定存在一个介于 4 到 5 之间的数 $p$,使得 $10^p=32768$,而对于一个复杂的乘法,比如 $32768\times 48597$,如果我们知道 $10^p=32768$,$10^q=48597$,那么乘积应该为 $10^{p+q}$。他把使得 $N=10^p$ 成立 $p$ 称为 $N$ 的对数,并且制作了“令人钦佩”的对数表,这时复杂的乘法只要查三次表再做一次简单的加法运算就可以完成了。这个方法虽然存在误差,但在当时仍然大大的优化的乘法的计算效率。我们关注的则是他和倒数曲线的面积一样有着把乘法变为加法的神奇性质。
就像我们定义圆的周长和直径的比值为 $\pi$ 一样,我们将正数 $x$ 的自然对数定义为面积 $A(x)$,也就是从 1 到 $x$ 之间倒数函数与坐标轴所夹的面积,并把它记为 $ln(x)$。这个对数的底数——自然对数的底——记为 $e$,因此我们有 $ln(e)=1$。值得注意的是,数学并不是将名称和缩写作为问题的答案,虽然我们用 $ln(x)$ 回答了问题 $dx/x$ 的积分是什么,但更重要的是,我们创造了对数函数的概念,并且它拥有 $ln(ab)=ln(a)+ln(b)$ 的优美性质。
我们已经知道对数函数简介的微分形式 $d ln(x)=dx/x$,那么其对应的指数函数 $e^x$ 的微分形式又是怎样的呢?如果我们写成 $y=e^x$, 我们有 $dx=dy/y$,因此 $dy=ydx$。我们发现 $e^x$ 的微分形式就是 $e^x dx$。也就是说这个函数在每一点的斜率都和函数值本身相等。自然对数和指数定义弥补了古典指数和对数概念的不足,让指数和对数成为了有连续性定义的基础函数。其奇特性质也成为高等数学教材中最重要的范例。
终于看完了

我想就到这里结束吧,这本名叫《度量》的书,书写了一些基础的微积分知识,从度量长度、面积和体积的角度出发,避开的复杂的概念和严格的证明,用大量巧妙和生动的例子描写了古典微积分和现代分析学的要领。数学是一门关于想象世界的学科,其美感不仅仅是巧妙变换的数字或者图形,而是从图形到数字的完美融合。
你可能也喜欢:


